I will discuss three approaches to find power(n, exp). power(n, exp) is defined as
power(2, 4) = 2 * 2 * 2 *2 = 16.
Iterative approach:
Space Complexity =&bg=FFFFFF&fg=000000&s=0) ;
;
Time Complexity =&bg=FFFFFF&fg=000000&s=0)
Divide and Conquer / Recursive approach:
While finding power(2, 20), we know that .
.
i.e, .
.
It means that we can find solution for power(n, exp/2) and multiply that value with it again.
...
temp = power(n, exp/2);
power(n, exp) = temp * temp;
...
That is how we can avoid recomputing power(n, exp/2) TWO times.
Space Complexity =&bg=FFFFFF&fg=000000&s=0) [ Used in Stack, while running the program ] ;
[ Used in Stack, while running the program ] ;
Time Complexity = O(log n)
Exponentiation by Squaring / (log n) Iterative Method:
Refer: Wiki: Exponentiation by Squaring
It seems Art of Computer Programming, Volume 2: Semi numerical Algorithms by Donald Knuth ( his books are generally Juggernaut ) has discussed this method in detail. You may refer it ( I have not yet ).
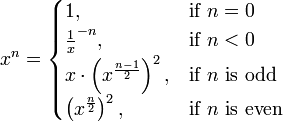
This approach is implementation of the equation shown above.
Space Complexity = O(1) ;
Time Complexity = O(log n)
This code will work only for exp > 0.
power(2, 4) = 2 * 2 * 2 *2 = 16.
Iterative approach:
Space Complexity =
Time Complexity =
result=1;
for(i=1 ; i<=exp ; i++) {
result *= n;
}
printf("Iterative method: [%d]\n", result);
Divide and Conquer / Recursive approach:
While finding power(2, 20), we know that
i.e,
It means that we can find solution for power(n, exp/2) and multiply that value with it again.
...
temp = power(n, exp/2);
power(n, exp) = temp * temp;
...
That is how we can avoid recomputing power(n, exp/2) TWO times.
Space Complexity =
Time Complexity = O(log n)
int rec_pow(int n, int exp) {
int subsoln;
if (exp==1) {
return n;
}
subsoln = rec_pow(n, exp/2);
if (exp & 1) {
// If exp is odd number.
return n * subsoln * subsoln;
}
return subsoln * subsoln;
}
Exponentiation by Squaring / (log n) Iterative Method:
Refer: Wiki: Exponentiation by Squaring
It seems Art of Computer Programming, Volume 2: Semi numerical Algorithms by Donald Knuth ( his books are generally Juggernaut ) has discussed this method in detail. You may refer it ( I have not yet ).
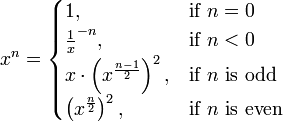
This approach is implementation of the equation shown above.
Space Complexity = O(1) ;
Time Complexity = O(log n)
This code will work only for exp > 0.
result=1;
while(exp) {
if (exp & 1) { // If exp is odd number.
result *= n;
}
exp >>= 1;
n *= n;
}
printf("Exponentiation by Squaring method: [%d]\n", result);